HISTÓRIA DA ÁLGEBRA
(uma visão geral)
Fonte: Tópicos de História da Matemática -
John K. Baumgart
A álgebra provavelmente se originou na Babilônia,
Estranha e intrigante é a origem da palavra "álgebra".
Ela não se sujeita a uma etimologia nítida como, por
exemplo, a palavra "aritmética", que deriva do
grego arithmos ("número"). Álgebra é
uma variante latina da palavra árabe al-jabr (às vezes
transliterada al-jebr), usada no título de um livro, Hisab
al-jabr w'al-muqabalah, escrito em Bagdá por volta do ano
825 pelo matemático árabe Mohammed ibn-Musa al Khowarizmi
(Maomé, filho de Moisés, de Khowarizm). Este trabalho
de álgebra é com frequência citado, abreviadamente,
como Al-jabr.
Uma tradução literal do título completo do
livro é a "ciência da restauração
(ou reunião) e redução", mas matematicamente
seria melhor "ciência da transposição e
cancelamento"- ou, conforme Boher, "a transposição
de termos subtraídos para o outro membro da equação"
e "o cancelamento de termos semelhantes (iguais) em membros
opostos da equação". Assim, dada a equação:
x2 + 5x + 4 = 4 - 2x + 5x3
al-jabr fornece
x2 + 7x + 4 = 4 + 5x3
e al-muqabalah fornece
x2 + 7x = 5x3
Talvez a melhor tradução fosse simplesmente "a
ciência das equações".
Ainda que originalmente "álgebra" refira-se a equações,
a palavra hoje tem um significado muito mais amplo, e uma definição
satisfatória requer um enfoque em duas fases:
(1) Álgebra antiga (elementar) é o estudo das equações
e métodos de resolvê-las.
(2) Álgebra moderna (abstrata) é o estudo das estruturas
matemáticas tais como grupos, anéis e corpos - para
mencionar apenas algumas.
De fato, é conveniente traçar o desenvolvimento da
álgebra em termos dessas duas fases, uma vez que a divisão
é tanto cronológica como conceitual.
Equações algébricas e notação
A fase antiga (elementar), que abrange o período de 1700
a.C. a 1700 d.C., aproximadamente, caracterizou-se pela invenção
gradual do simbolismo e pela resolução de equações
(em geral coeficientes numéricos) por vários métodos,
apresentando progressos pouco importantes até a resolução
"geral" das equações cúbicas e quárticas
e o inspirado tratamento das equações polinomiais
em geral feito por François Viète, também conhecido
por Vieta (1540-1603).
O desenvolvimento da notação algébrica evoluiu
ao longo de três estágios: o retórico (ou verbal),
o sincopado (no qual eram usadas abreviações de palavras)
e o simbólico. No último estágio, a notação
passou por várias modificações e mudanças,
até tornar-se razoavelmente estável ao tempo de Isaac
Newton. É interessante notar que, mesmo hoje, não
há total uniformidade no uso de símbolos. Por exemplo,
os americanos escrevem "3.1416" como aproximação
de Pi, e muitos europeus escrevem "3,1416". Em alguns
países europeus, o símbolo "÷" significa
"menos".
Antes de deixar a álgebra babilônica, notemos que
eles eram capazes de resolver uma variedade surpreendente de equações,
inclusive certos tipos especiais de cúbicas e quárticas
- todas com coeficientes numéricos, naturalmente.
Álgebra no Egito
A álgebra surgiu no Egito quase ao mesmo tempo que na Babilônia;
mas faltavam à álgebra egípcia os métodos
sofisticados da álgebra babilônica, bem como a variedade
de equações resolvidas, a julgar pelo Papiro Moscou
e o Papiro Rhind - documentos egípcios que datam de cerca
de 1850 a.C. e 1650 a.C., respectivamente, mas refletem métodos
matemáticos de um período anterior. Para equações
lineares, os egípcios usavam um método de resolução
consistindo em uma estimativa inicial seguida de uma correção
final - um método ao qual os europeus posteriormente deram
o nome umtanto abstruso de "regra da falsa posição".
A álgebra do Egito, como a da Babilônia, era retórica.
O sistema de numeração egípcio, relativamente
primitivo em comparação com o dos babilônios,
ajuda a explicar a falta de sofisticação da álgebra
egípcia. Os matemáticos europeus do século
XVI tiveram de estender a noção indo-arábica
de número antes de poderem avançar significativamente
além dos resultados babilônios de resolução
de equações.
Álgebra geométrica grega
A álgebra grega conforme foi formulada pelos pitagóricos
e por Euclides era geométrica. Por exemplo, o que nós
escrevemos como:
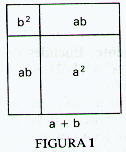
(a+b)2 = a2 + 2ab + b2
era concebido pelos gregos em termos do diagrama apresentado na
Figura 1 e era curiosamente enunciado por Euclides em Elementos,
livro II, proposição 4:
Se uma linha reta é dividida em duas partes quaisquer, o
quadrado sobre a linha toda é igual aos quadrados sobre as
duas partes, junto com duas vezes o retângulo que as partes
contém. [Isto é, (a+b)2 = a2 + 2ab + b2.]
Somos tentados a dizer que, para os gregos da época de Euclides,
a2 era realmente um quadrado.
Não há dúvida de que os pitagóricos
conheciam bem a álgebra babilônica e, de fato, seguiam
os métodos-padrão babilônios de resolução
de equações. Euclides deixou registrados esses resultados
pitagóricos. Para ilustrá-lo, escolhemos o teorema
correspondente ao problema babilônio considerado acima.
Do livro VI dos Elementos, temos a proposição 28
(uma versão simplificada):
Dada uma linha reta AB [isto é, x+y=k], construir ao longo
dessa linha um retângulo com uma dada área [xy = P],
admitindo que o retângulo "fique aquém" em
AB por uma quantidade "preenchida" por outro retângulo
[o quadrado BF na Figura 2], semelhante a um dado retângulo
[que aqui nós admitimos ser qualquer quadrado].
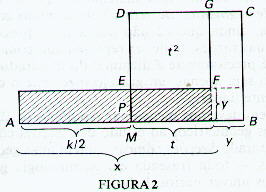
Na solução desta construção solicitada
(Fig.2) o trabalho de Euclides é quase exatamente paralelo
à solução babilônica do problema equivalente.
Conforme indicado por T.L.Heath / EUCLID: II, 263/, os passos são
os seguintes:
Bissecte AB em M: k/2
Construa o quadrado MBCD: (k/2)2
Usando VI, 25, construa o quadrado DEFG com área igual ao
excesso de MBCD sobre a área dada P: t2 = (k/2)2 - P
Então é claro que y = (k/2) - t
Como fazia frequentemente, Euclides deixou o outro caso para o
estudante - neste caso, x=(k/2)+t, o que Euclides certamente percebeu
mas não formulou.
É de fato notável que a maior parte dos problemas-padrão
babilônicos tenham sido "refeitos" desse modo por
Euclides. Mas por quê? O que levou os gregos a darem à
sua álgebra esta formulação desajeitada? A
resposta é básica: eles tinham dificuldades conceituais
com frações e números irracionais.
Mesmo que os matemáticos gregos fossem capazes de contornar
as frações, tratando-as como razões de inteiros,
eles tinham dificuldades insuperáveis com números
como a raiz quadrada de 2, por exemplo. Lembramos o "escândalo
lógico" dos pitagóricos quando descobriram que
a diagonal de um quadrado unitário é incomensurável
com o lado (ou seja, diag/lado é diferente da razão
de dois inteiros).
Assim, foi seu estrito rigor matemático que os forçou
a usar um conjunto de segmentos de reta como domínio conveniente
de elementos. Pois, ainda que raiz quadrada de 2 não possa
ser expresso em termos de inteiros ou suas razões, pode ser
representado como um segmento de reta que é precisamente
a diagonal do quadrado unitário. Talvez não seja apenas
um gracejo dizer que o contínuo linear era literalmente linear.
De passagem devemos mencionar Apolônio (c. 225 a.C.), que
aplicou métodos geométricos ao estudo das secções
cônicas. De fato, seu grande tratado Secções
cônicas contém mais geometria analítica das
cônicas - toda fraseada em terminologia geométrica
- do que os cursos universitários de hoje.
A matemática grega deu uma parada brusca. A ocupação
romana tinha começado, e não encorajava a erudição
matemática, ainda que estimulasse alguns outros ramos da
cultura grega. Devido ao estilo pesado da álgebra geométrica,
esta não poderia sobreviver somente na tradição
escrita; necessitava de um meio de comunicação vivo,
oral. Era possível seguir o fluxo de idéias desde
que um instrutor apontasse para diagramas e explicasse; mas as escolas
de instrução direta não sobreviveram.
Álgebra na Europa
A álgebra que entrou na Europa (via Liber abaci de Fibonacci
e traduções) havia regredido tanto em estilo como
em conteúdo. O semi-simbolismo (sincopação)
de Diofanto e Brahmagupta e suas realizações relativamente
avançadas não estavam destinados a contribuir para
uma eventual irrupção da álgebra.
A renascença e o rápido florescimento da álgebra
na Europa foram devidos aos seguintes fatores:
facilidade de manipular trabalhos numéricos através
do sistema de numeração indo-arábico, muito
superior aos sistemas (tais como o romano) que requeriam o uso do
ábaco;
invenção da imprensa com tipos móveis, que
acelerou a padronização do simbolismo mediante a melhoria
das comunicações, baseada em ampla distribuição;
ressurgimento da economia, sustentando a atividade intelectual;
e a retomada do comércio e viagens, facilitando o intercâmbio
de idéias tanto quanto de bens.
Cidades comercialmente fortes surgiram primeiro na Itália,
e foi lá que o renascimento algébrico na Europa efetivamente
teve início.
ATENÇÃO : Se você precisa de uma pesquisa que
não está listada aqui, mande um e-mail para : [email protected]
e nós vamos procurar o assunto e incluir na lista.