|
|
|
Aula
particular de Matemática
no
Rio de Janeiro presencial ou pela webcam
50
série até o pré-vestibular
Tel:
98899 - 8100 [email protected]
|
|
|
|
DISCURSIVA UERJ 2010
|
|
|
|
|
|
|
|
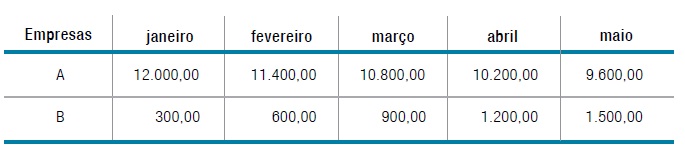
1) Duas empresas, A e B, farão doações mensais a uma creche. A tabela abaixo mostra os
valores, em reais, dos depósitos iniciais, a serem realizados nos cinco primeiros meses
de 2010.
Empresasjaneiro fevereiro março abril maio
A 12.000,00 11.400,00 10.800,00 10.200,00 9.600,00
B 300,00 600,00 900,00 1.200,00 1.500,00
|
|
|
|
A diferença entre os valores depositados pelas empresas entre dois meses subsequentes
será mantida constante ao longo de um determinado período.
Determine o mês e o ano desse período em que o valor mensal do depósito da empresa A
será igual ao da empresa B. Resolução
|
|
|
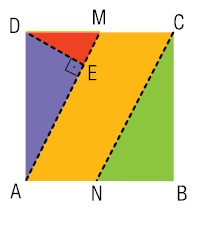
2) Observe a figura abaixo, que representa um quadrado ABCD, de papel, no qual M e N são os
pontos médios de dois de seus lados. Esse quadrado foi dividido em quatro partes para
formar um jogo.
|
|
|
O jogo consiste em montar, com todas essas partes, um retângulo cuja base seja maior que
a altura. O retângulo PQRS, mostrado a seguir, resolve o problema proposto no jogo.
|
|

|
|
calcule a razão: PS/PQ
|
|
Resolução
|
|
|
|
3) Um cofre eletrônico possui um painel com dez teclas numéricas e pode ser aberto por meio da digitação, em
qualquer ordem, de três teclas distintas dentre seis habilitadas previamente pelo fabricante.
Considere n o número máximo de conjuntos distintos de três teclas que abrem o cofre.
Na figura em destaque, as teclas azuis representam as habilitadas previamente.
|
|

|
Se o fabricante reduzisse para cinco o número de teclas habilitadas, haveria entre elas um total de
m conjuntos distintos de três teclas distintas para abrir o cofre.
Calcule o valor de n - m. Resolução
|
|
|
|
4) Uma criança guarda moedas de R$ 1,00 e de R$ 0,50 em duas caixas, uma verde e outra amarela. Na caixa
amarela, há, exatamente, 12 moedas de R$ 1,00 e 15 moedas de R$ 0,50. Admita que, após a transferência de n
moedas de R$ 1,00 da caixa verde para a amarela, a probabilidade de se retirar ao acaso uma moeda de R$ 1,00 da caixa amarela seja igual a 50%.
Calcule o valor de n. Resolução
|
|
|
|
|
|
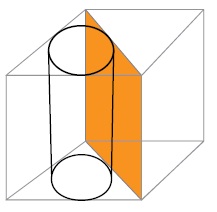
5) Uma caixa cúbica foi dividida em duas partes por um plano que contém duas diagonais de faces opostas
da caixa. Uma das partes acomoda, sem folga, uma lata com a forma de um cilindro circular reto, conforme
ilustrado abaixo.
|
|
|
Desprezando as espessuras dos materiais utilizados na lata, na caixa e na divisória, calcule a razão entre o
volume do cilindro e o da caixa. Resolução
|
|
|
|
|
6) Sejam a e b dois números reais positivos e A, G e H, respectivamente, as médias aritmética, geométrica
e harmônica desses dois números. Admita que a > b
e que a sequência (A, G, H) seja uma progressão geométrica de razão 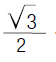
|
determine 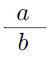 Resolução
Resolução
|
|
|
|
|
|
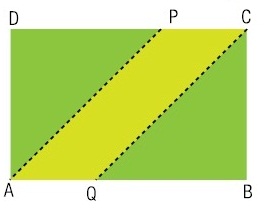
7) Um terreno retangular tem 800 m de perímetro e será dividido pelos segmentos PA e CQ em três partes, como
mostra a figura.
|
|
|
Admita que os segmentos de reta PA e CQ estão contidos nas bissetrizes de dois ângulos retos do terreno e
que a área do paralelogramo PAQC tem medida S.
Determine o maior valor, em m2, que S pode assumir. Resolução
|
|
|
8) Ao final de um campeonato de futebol, foram premiados todos os jogadores que marcaram 13, 14 ou 15 gols
cada um. O número total de gols realizados pelos premiados foi igual a 125 e, desses atletas, apenas cinco
marcaram mais de 13 gols.
Calcule o número de atletas que fizeram 15 gols. Resolução
|
|
|
9) Suponha que x e y são números reais positivos que apresentam logaritmos com bases diferentes, conforme
as igualdades a seguir:
log9 x = log6 y = log4 (x+y)
Calcule a razão y/ x Resolução
|
|
|
|
|
|
10) As seis soluções da equação z6+ z3 + 1 = 0 são números complexos que possuem módulos iguais e
argumentos distintos.
O argumento ., em radianos, de uma dessas soluções pertence ao intervalo
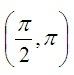
Determine a medida de 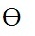 Resolução Resolução
|






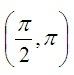
![]() Resolução
Resolução